Jenner's Blog

不变秃，也要变强！

0%

数字签名

发表于 更新于 分类于 ， Valine：

数字签名在区块链中主要运用在交易签名上。

RSA（模幂运算）

根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥.

算法描述

RSA算法的具体描述如下：

（1）任意选取两个不同的大素数p和q计算乘积$n=pq, φ(n)=(p-1)(q-1);$

n的二进制长度是密钥长度。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

（2）任意选取一个大整数e，满足 gcd(e,φ(n)) = 1，1< e < φ(n)，整数e用做加密钥（注意：e的选取是很容易的，例如，所有大于p和q的素数都可用）；

（3）确定的解密钥d，满足 (de)mod φ(n) = 1 ，即de = kφ(n) +1, k≥1是一个任意的整数；所以，若知道e和φ(n)，则很容易计算出d；

（4）公开整数n和e，秘密保存d ；

（5）将明文m（m<n是一个整数）加密成密文c，加密算法为$c=E(m)=m^emodn$ , n和e为公钥；

（6）将密文c解密为明文m，解密算法为$m=D(c)=c^dmodn$，n和d为私钥；

然而只根据n和e（注意：不是p和q）要计算出d是不可能的。因此，任何人都可对明文进行加密，但只有授权用户（知道d）才可对密文解密。

RSA签名验证

RSA密码体制既可以用于加密又可以用于数字签名。下面介绍RSA数字签名的功能。

已知公钥（e，n），私钥d

  • 1.对于消息m签名为：sign ≡ m ^d mod n
  • 2.验证：对于消息签名对（m，sign），如果m ≡ sign ^e mod n，则sign是m的有效签名

这里的c是明文m。

证明：c=(((c^e)%n)^d)%n

(((c^e)%n)^d)%n =(c^(d*e))%n =(c^(k*t+1))%n =(c*((c^k)^t))%n =((c%n)*(((c^k)^t)%n))%n =((c%n)*(((c^k)%n)^t)%n)%n

ϕ(n)是欧拉函数，ϕ(n)=从1到n-1中所有与n互质整数的个数。k=ϕ(n)。根据欧拉定理(1)，对于任意c，如果c与n互质，那么：(c^k)%n=(c^ϕ(n))%n=1

因此，

1
2
3
4
5
6
7
((c%n)*(((c^k)%n)^t)%n)%n

=((c%n)*((1^t)%n))%n

=((c%n)*1)%n

=c%n

因为c与n互质，所以c%n=c，也就是说：

(((c^e)%n)^d)%n=c

ECC（几何离散）

阶：一个群的点的数量；在循环子群中，P的阶是最小的正整数n，n使得nP=0；

如何根据基点 P 找到子群的阶：

  1. 使用Schoof的算法去计算椭圆曲线的阶 N 。
  2. 找到 N 所有的因子。
  3. 对于 N 的每一个因子 n ,计算 nP 。
  4. 找到最小的且满足 nP=0 的 n , n 就是子群的阶。

NP=n(hP)=0 , 令G=hP => nG=0

找基点

  1. 计算椭圆曲线的阶 N 。
  2. 选择一个阶为 n 的子群。n必须是素数且必须是 N 的因子。
  3. 计算辅因子 h = N / n 。
  4. 在曲线上选择一个随机的点 P 。
  5. 计算 G = hP 。
  6. 如果 G 是0，那么回到步骤4。否则我们就已经找到了阶为 n 和辅因子是 h 的子群的基点。

私钥：d , {1…n-1}； 公钥：H=dG

ECDH

  1. Alice 和 Bob 生成各自的私钥和公钥，Alice 的私钥为 $d_A$ ，公钥为 $H_A = d_AG$ 。Bob 的私钥为 $d_B$，公钥为 $H_B = d_BG$ ，注意，Alice 和 Bob 需要使用一样的主要参数：在同一条曲线的同一个有限域上选择一样的基点 G。
  2. Alice 和 Bob 通过不安全信道交换各自的公钥$H_A$和 $H_B$ ，中间人可以窃听到 $H_A$和 $H_B$，但是在无法攻破离散对数难题的情况下无法得到 $d_A$ 和 $d_B$ 。
  3. Alice 计算 $S=d_AH_B$ （使用自身的私钥和 Bob 的公钥），Bob 计算 $S=d_BH_A$ （使用自身的私钥和 Alice 的公钥），双方求得的 S 是一样的，因为 $S=d_AH_B=d_A(d_BG)=d_B(d_AG)=d_BH_A$

举个栗子，他们可以使用 S 的 x 轴坐标作为 AES 或者 3DES 的密钥来加密信息，这多少有点像是 TLS 的操作，不同点是 TLS 将 x 轴坐标和网络连接相关的其他参数串联起来，然后计算这个串的哈希值。

ECDSA

Alice 想要使用她的私钥 $d_A$ 来签名，Bob 想用 Alice 的公钥 $H_A$ 要验证签名，只有 Alice 才能提供正确的签名，而每个人都可以验证签名。

Alice 使用算法来签名的步骤如下：

  1. 在 {1,…, n-1} 范围内选取一个随机数 k （ n 是子群的阶）
  2. 计算点 P=kG（ G 是子群的基点）
  3. 计算数字 $r = x_p[mod]n$ （ $x_p$是p的x轴坐标）
  4. 如果 r=0 ，另选一个 k 并重新计算
  5. 计算 $s=k^{-1}(z+rd_A)[mod]n$ （ $d_A$是 Alice 的私钥， $k^{-1}$是 k mod n 的乘法逆元）
  6. 如果 s=0 ，另选一个 k 并重新计算

(r, s) 就是签名。

验证签名

为了验证签名，我们需要 Alice 的公钥 $H_A$ ，被截断的哈希值 z，还有签名 (r, s)

  1. 计算整数 $u_1 = s^{-1}z [mod] n$
  2. 计算整数 $u_2 = s^{-1}r[mod]n$
  3. 计算点 $P=u_1G + u_2H_A$

只有当 $r=x_P[mod]n$ 的时候，签名才被成功验证

算法的正确性

算法的逻辑一开始看不是很容易理解，如果我们把前面用到的公式整合联立一下，就变得清晰了

我们从 $P=u_1G + u_2H_A$ 开始，通过公钥的定义我们知道 $H_A = d_A G$ （ $d_A$是私钥），所以我们得到：

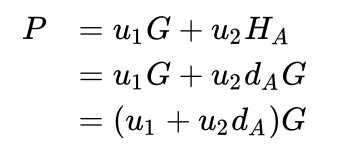
image-20200909163306958

使用 $u_1$ 和 $u2$的定义，可以得到：

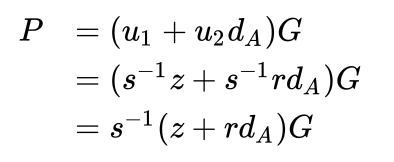
image-20200909163321840

这里为了简单先忽略 mod n ，因为由 G 生成的循环子群的阶为 n ，所以这里的 mod n 其实也是没必要的。

再往前，我们定义了 $s = k^{-1}(z+rd_A)[mod]n$ ，式子两边同乘以 k再同除 s，也就是:$k=s^{-1}(z+rd_A)[mod]n$，把这个结果带到上面关于 P 的等式中得到：

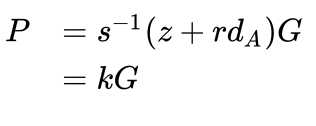
image-20200909163510588

Schnorr

我们定义几个变量：

  • G：椭圆曲线基点。
  • m：待签名的数据，通常是一个32字节的哈希值。
  • x：私钥。P = xG，P为x对应的公钥。
  • H()：哈希函数。
    • 示例：写法H(m || R || P)可理解为：将m, R, P三个字段拼接在一起然后再做哈希运算。

生成签名

签名者已知的是：G-椭圆曲线基点, H()-哈希函数，m-待签名消息, x-私钥。

  1. 选择一个随机数k, 令 R = k*G
  2. 令 s = k + H(m || R || P)*x

那么，公钥P对消息m的签名就是：(R, s)，这一对值即为Schnorr签名。

验证签名

验证者已知的是：G-椭圆曲线, H()-哈希函数，m-待签名消息, P-公钥，(R, s)-Schnorr签名。验证如下等式：

s*G = R + H(m || R || P)P

若等式成立，则可证明签名合法。

我们推演一下，此过程包含了一个极其重要的理论：椭圆曲线无法进行除法运算。

  1. s值的定义：s = k + H(m || R || P)*x，等式两边都乘以椭圆曲线G，则有：
  2. sG = kG + H(m || R || P)*x*G，又因R = kG, P = xG，则有：
  3. sG = R + H(m || R || P)P，椭圆曲线无法进行除法运算，所以第3步的等式，无法向前反推出第1步，就不会暴露k值以及x私钥。同时，也完成了等式验证。

组签, Group Signature

一组公钥，N把，签名后得到N个签名。这个N个签名是可以相加的，最终得到一个签名。这个签名的验证通过，则代表N把公钥的签名全部验证通过。

有：

  • 椭圆曲线基点：G
  • 待签名的数据：m
  • 哈希函数：H()
  • 私钥：x1，x2，公钥：P1=x1G, P2=x2G
  • 随机数：k1, k2，并有 R1=k1G, R2=k2G
  • 组公钥：P = P1 + P2

则有：

  • 私钥x1和x2的签名为：(R1, s1), (R2, s2)。
  • 两个签名相加得到组签名：(R, s)。其中：R = R1 + R2, s = s1 + s2。

推演过程：

  1. 令R = R1 + R2, s = s1 + s2

  2. 已知：s1 = k1 + H(m || R || P)*x1，s2 = k2 + H(m || R || P)*x2

  3. 1
    2
    3
    4
    5
    s = s1 + s2

       = k1 + H(m || R || P)*x1 + k2 + H(m || R || P)*x2

       = (k1 + k2) + H(m || R || P)(x1 + x2)

  4. 两边同时乘以G，则有：

    1
    2
    3
    4
    sG = (k1 + k2)G + H(m || R || P)(x1 + x2)G
    	= (k1G + k2G) + H(m || R || P)(x1G + x2G)
    	= (R1 + R2) + H(m || R || P)(P1 + P2)
    	= R + H(m || R || P)P

  5. 完成证明，并从两个合作方推演至N个合作方

组公钥(Group Key)，是N把公钥进行相加后的值，又称聚合公钥(Aggregation Key)。需要指出的是，参与方需要先相互交换公钥和R值，然后再进行各自的签名。

多签

聚合签名对应于聚合公钥。但是，我们不只是将所有联合签名者的公钥相加，而是将它们乘以某个因子。聚合的公钥将是P=hash(L,P1)×P1+…+hash(L,Pn)×Pn。这里L=hash(P1,…,Pn)是一个取决于所有公钥的公用数字。这种非线性特性可以防止攻击者构造一个不好的公钥，例如在恶意密钥攻击当中。尽管攻击者知道自己的哈希 (L,Patk)×Patk 应是什么，但他不能从中派生 Patk，这和从公钥派生私钥是相同的问题。

m-of-n多重签名使用默克尔树；

BLS

Boneh-Lynn-Shacham

Schnorr 签名方案是非常了不起的，如果我们做得对，我们可以将交易中的所有签名和公钥组合为一个密钥和一个签名，没有人会发现它们对应于多个密钥。区块验证也可以变得更快，因为我们可一次性验证所有签名。但它也存在着一些问题：

  1. 多重签名方案需要多轮通信，这会使冷存储变得非常烦人；
  2. 对于签名聚合，我们必须依赖随机数生成器，我们不能像在 ECDSA 中那样确定地选择随机点 R；
  3. m-of-n 多重签名方案是棘手的，我们需要制作一个公共密钥的默克尔树（merkle tree），对于大数的 m 和 n 来说，这颗默克尔树可以变得相当大；
  4. 我们不能将区块中的所有签名组合为单个签名；

BLS 签名可修复上述所有问题，我们不需要随机数，区块中的所有签名都可以组合成单个签名，m-of-n 类型的多重签名非常简单，我们不需要签名者之间进行多轮通信。此外，BLS 签名相比 Schnorr 签名或 ECDSA 签名要小 2 倍，其签名不是一对，而是一个单曲线点。

私钥：pk，公钥 P=pkG， 签名消息是m，消息哈希到曲线H(m)，签名：S=pkH(m)

验证：e(P,H(m)) = e(G,S)

和 Schnorr 签名方案一样，运用 BLS 签名需要保护自己免受流氓密钥攻击。我们可通过要求每个联合签名者证明他们具有的公钥的私钥（通过签名他们的公钥），或者我们可以在方案中添加一些非线性元素，使恶意密钥攻击成为不可能。我们不是简单地将所有的密钥和签名相加，而是将它们乘以一个特定的数字，然后再相加：

S = a1×S1+a2×S2+a3×S3

P = a1×P1+a2×P2+a3×P3

在这里，签名和密钥的系数是根据签名者的公钥和所有其他公钥来确定计算的：

ai = hash(Pi, {P1,P2,P3})

这个方案的好处在于，你不需要在设备之间进行多轮通信。你只需要知道谁是其他签名者。这比 Schnorr 签名的 3 轮多重签名方案要简单得多。它也不依赖任何随机性，它是一种完全确定的签名算法。

m-of-n签名

我们的每个设备都有一个签名者编号 i=1,2,3，代表其在集合中的位置，一个私钥 pki 以及一个对应的公钥 Pi = pki×G。这里计算聚合公钥的方式与之前完全相同：

P = a1×P1+a2×P2+a3×P3, ai = hash(Pi, {P1,P2,P3})

现在，每个设备都需要签名，而编号 i 是我们的聚合公钥的成员（对于每个 i），聚合这些签名并将结果保存到相应的设备上：

MKi = (a1⋅pk1)×H(P, i)+(a2⋅pk2)×H(P, i)+(a3⋅pk3)×H(P, i)

这个签名我们称为“成员密钥”，稍后我们将使用它进行签名。每个成员密钥都是消息 H(P,i) 的有效 n-of-n 签名，这意味着：

e(G, MKi)=e(P, H(P,i))

记住这个方程，我们以后会用到的。它将用来证明我们是多重签名方案的有效参与者。

签名

现在假设我们只想用密钥 pk1 和 pk3 签署一笔交易。我们生成两个签名 S1 和 S3:

S1 = pk1×H(P, m)+MK1, S3=pk3×H(P, m)+MK3

并将它们相加以获得单个签名和密钥：

(S’, P’) = (S1+S3, P1+P3)

我在这里写为 P’ 和 S’，来强调这个密钥和签名只由签名者的一个子集签名，它与 P 不同，P 是所有签名者的聚合密钥。要验证这 3 个签名中的 2 个，我们需要检查：

e(G, S’) = e(P’, H(P, m))⋅e(P, H(P, 1)+H(P, 3))

我们记得成员密钥 MK1 和 MK3 是由聚合密钥 P 签名的消息 H(P, 1) 及 H(P, 3) 的有效签名，因此：

e(G, S’) = e(G, S1+S3)=e(G, pk1×H(P, m)+pk3×H(P, m)+MK1+MK3) =e(G, pk1×H(P,m)+pk3×H(P, m))⋅e(G, MK1+MK3)=e(pk1×G+pk3×G, H(P, m))⋅e(P, H(P, 1)+H(P,3))=e(P’, H(P, m))⋅e(P, H(P, 1)+H(P, 3))

BLS 签名的弊端：配对效率低下。

VRF

全称为Verifiable Random Functionn。

可验证随机函数一共包含四个函数：1、生成密钥，生成一个公钥私钥对；2、生成随机数输出；3、计算零知识证明；4、验证随机数输出。

证明人用私钥和随机数r计算证明s,t，私钥可以确定得到随机数v，发送（随机数v，证明哈希，t)。验证者不需要知道证明人的私钥和随机数r，就可以验证随机数生成是否正确。

点击下方打赏按钮，获得支付宝二维码